Irreducibility of Galois representations attached to Elliptic Curves

Epistemic status: I have not checked this carefully for errors, it is entirely possible there are mistakes in this.

We will be mostly be concerned with Elliptic curves over number fields $E/K$ . However, let us start with a general lemma about Elliptic curves with endomorphism ring $\mathbb Z$ . In this post, I collect some properties about representations coming from Elliptic curves.

Lemma 1: Let $E$ be an elliptic curve over a field with endomorphism ring exactly $\mathbb Z$ . Then for elliptic curves $E',E''$ with isogenies $f',f'': E',E'' \to E$ with non isomorphic cyclic kernels, then $E',E''$ are not isomorphic.

Proof: Say the kernels have degree $n',n''$ and suppose $E',E''$ are isomorphic. Consider the isogeny $g: E \to E' \to E'' \to E$ where the central arrow is the supposed isomorphism and the last arrow is the dual of $f''$ . This is an endomorphism of $E$ and therefore, by assumption is of the form $[n]$ (multiplication by $n$ ).

Moreover, the kernel of $g$ contains the kernel of $f'$ which is a cyclic subgroup. Therefore, $\mathbb Z/n'\mathbb Z$ is contained in $\mathbb Z/a\mathbb Z$ . That is, $n'|a$ . Moreover, the quotient by the kernel of $f$ contains the cyclic subgroup $\mathbb Z/n''\mathbb Z$ . By a similar argument, this shows that $n''|a$ .

That is to say, $n'n'' = a^2$ and $n',n''|a$ and therefore $n'=n''$ contrary to assumption.

$\Box$

This might seem like quite a specialized lemma but it has surprising utility. For instance, this lemma features implicitly in showing that the various definitions of a supersingular elliptic curve are equivalent. We will use it together with Shafarevich’s theorem to prove the irreducibility of the Galois representation on the Tate module.

Theorem 1[Shafarevich’s Theorem]: If $E$ is an elliptic curve over a number field $K$ and $S$ is a finite set of finite places of $K$ , then there are only finitely many isomorphism classes of Elliptic curves with good reduction away from $S$ .

This has the important corollary:

Corollary 1: There are only finitely many isomorphism classes of Elliptic curves isogenous to $E/K$ .

I will not prove either theorem here but the proofs are not too hard. The idea is to bound the number of Elliptic curves that can occur by considering the Weierstrass equation and showing that there are only finitely many options that can occur for any given discriminant (by Siegel’s theorem). The number of discriminants that can occur is further bounded since they are units in $\mathscr O_{K,S}$ determined upto a 12th power.

We can use the lemma and corollary to prove the irreducibility of Galois representations. Let $V_l$ be the rational Tate module of $E$ and $E[l]$ the $l-$ torsion of $E$ . Both of these are $G_K = \mathrm{Gal}(\overline K/K)$ modules.

Theorem 2: For curves $E/K$ with no (rational) Complex multiplication, $V_l$ is irreducible for all $l$ and $E[l]$ is irreducible for almost all $l$ .

Proof: If $E[l]$ is reducible, then it contains a cyclic submodule $X_l$ defined over $K$ . Then, $E/X_l$ are elliptic curves defined over $K$ , isogenous to $E$ with cyclic kernels of order $l$ and therefore by the lemma are pairwise non isomorphic. However, by the corollary, there can only be finitely many such isomorphism classes and therefore, finitely many $l$ such that $E[l]$ is reducible.

Similarly, suppose $V_l$ is reducible. Then it contains a cyclic submodule $Y$ . Since the integral Tate module $T_l$ is also Galois-invariant, we can define $X = Y_l \cap T_l$ defined over $K$ . Consider $X_n = X/l^nX$ . These are cyclic subgroups of $E[l^n]$ . As such, we can define $E_n = E/X_n$ to be curves over $K$ isogenous to $E$ with cyclic kernels.

As before, by the lemma they are pairwise distinct but by Shafarevich’s theorem this is impossible. In this case, we can also avoid Shafarevich’s theorem by the following argument:

By the lemma, we know that there $E_n \cong E_m$ for some $m>n$ . Note that $X_n \subset X_m$ in this case. Therefore, there is an isogeny $E/X_n \to E/X_m$ with cyclic kernel but this is also an endomorphism since these curves were assumed to be isomorphic. Since $E/X_n$ does not have CM by assumption, this is an impossibility (endomorphisms cannot have cyclic kernels in this case).

$\Box$

This theorem is quite interesting but also quite far from the best known. A few remarks follow:

Remark 1: The above theorem is false for curves with complex multiplication. In that case, suppose $K$ is a field that contains the field of endomorphisms $L$ of $E$ . If $p = \pi_1\pi_2$ is a prime that splits in $L$ , then $E[p]$ is reducible. This is because there exists an isogeny $[\pi_1]$ defined over $K$ with kernel of size $N(\pi_1) = p$ .

Remark 2: In fact, the assumption of not having rational CM is not hard to achieve at all. For instance, suppose our base field does not contain any quadratic imaginary number field (for instance, it could be $\mathbb Q$ or a totally real number field more generally), then by studying the action on the tangent space, it is easy to see that the endomorphism ring is always $\mathbb Z$ .

Remark 3: Serre proved a much stronger version of this where he showed that, under the hypothesis of the theorem, the image of $G_K$ in the $E[l]$ is in fact isomorphic to the entire group $GL_2(\mathbb F_p)$ for almost all $l$ . This is proved in his famous 1972 paper “Proprites galoisiennes des points d’ordre fini des courbes elliptiques”. This is of course much stronger than simple irreducibility.

In fact, we can beef up irreducibility to absolute irreducibility easily enough:

First, note that there is an element (called complex conjugation) in $G_K$ that has order $2$ and determinant $-1$ by the Weil pairing. Hence, it has eigenvalues $1,-1$ . In particular, we can find a rational basis of eigenvectors for complex conjugation. Since the action on $E[l]$ is by the reduction of the action on $V_l$ , the same is true for the characteristic $l$ reduction.

This is to say, we have an element that has two eigenvectors with eigenvalues $1,-1$ defined over the base field. This is sufficient to prove absolute irreducibility:

Corollary 3: Let $V$ be a two dimensional irreducible representation of a group $G$ over the field $K$ . Suppose that there is an element $g$ with two eigenvectors $v,w$ with eigenvalues $1,-1$ respectively. Then, the representation is absolutely irreducible.

Proof: Let $L/K$ be a field extension such that $V\otimes_K L$ is reducible. Then, there is an invariant subspace generated by a vector of the form $\alpha v + \beta w$ . In particular, $g$ fixes it which implies that $\alpha$ or $\beta$ is $0$ .

However, this immediately implies that the vector space spanned by $v$ or $w$ in $V$ is in fact invariant under $G$ and hence $V$ is irreducible.

$\Box$

4 thoughts on “Irreducibility of Galois representations attached to Elliptic Curves”

Ari

March 21, 2019 at 4:59 pm

Should the very last word of the post be “reducible” instead of “irreducible”?

LikeLike

- Asvin G.
  
  March 21, 2019 at 5:22 pm
  
  You are right!
  
  LikeLike
  
alexyoucis

November 29, 2019 at 12:38 am

You want to be careful about what you mean by CM. Let’s say that $E/K$ ( $K$ a number field) has ‘rational CM’ if $\mathrm{End}(E)\supsetneq \mathbb{Z}$ and that it has ‘geometric CM’ if $E_{\overline{K}}$ has CM. For Theorem 2 and Remark 1 I think you want to refer to rational CM.

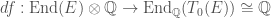You might also point out that not only is the assumption that E has no rational CM not restrictive it applies, for examlpe, to *every* elliptic curve if $K=\mathbb{Q}$ . 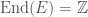Indeed, one can check that if $E/K$ is an elliptic curve the map $df:\mathrm{End}(E)\otimes\mathbb{Q}\to \mathrm{End}_\mathbb{Q}(T_0(E))\cong\mathbb{Q}$ is a ring map and thus $\mathrm{End}\otimes\mathbb{Q}=\mathbb{Q}$ which implies that $\mathrm{End}(E)=\mathbb{Z}$ .

LikeLike

- Asvin G.
  
  November 30, 2019 at 6:33 pm
  
  Yes, you are right. Thanks for the suggestions!
  
  LikeLike